5分钟讲清楚ABtset，详解数据分析必备模型——辛普森悖论!

假设你是一个APP的负责人，你的团队成员在争吵不休。因为一个页面的设计修改，你现在面临一个选择问题:选择方案A是否更好？B计划更好吗？

今天介绍的分析思维模型:A/B测试模型可以帮助你做出更科学的选择。

1.模型介绍

A/B测试是将优化前和优化后的方案在同一时间段展示给同类用户，通过数据分析判断是否符合预期的测试方法。

广告界有一句经典的话:

我知道广告的投入有一半是没用的，但问题是我不知道是哪一半。

这句话在传统广告行业一直都是成立的。

但随着互联网的发展，人们可以快速获取大量的用户行为数据，从而准确衡量广告的效果，减少无效广告的投放。这背后的关键技术是A/B测试模型。

互联网时代，细节决定成败。

谷歌、脸书、字节跳动等知名互联网公司正在广泛应用A/B测试。无论是色彩调整、位置摆放还是文案设计，很多细节都会通过A/B测试来验证，从而实现产品的不断优化。2.应用示例

A/B测试广泛应用于互联网、医疗、金融等领域。以APP设计方案的选择为例:

首先要明确指标是什么，比如转化率高就代表好。

其次，要合理划分流量，保证A组和B组的用户特征基本一致，并且两者都具有代表性，能够代表整体用户特征。

如果整体流量比较大，为了减少测试可能造成的损失，建议在测试初期小范围尝试，比如取2%的流量，其中1%的用户为A组，1%的用户为b组。

当流量足够大时，可以根据用户的特征(如年龄、性别等)将用户划分为更细致的用户群。)分别进行A/B测试，尽量排除其他因素的干扰。

然后，通过数据分析，比较检验结果，并做显著性检验。

可以使用在线AB测试结果分析工具输入访问次数和转化次数，可以自动计算转化率和统计显著值。

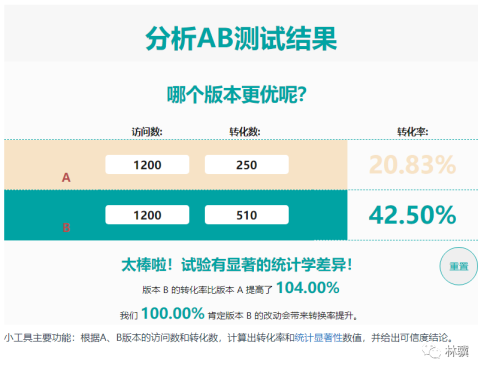
如果测试结果不显著，可能是由于样本量不足。建议增加检验的比重，以便得到更明确的检验结果，从而指导下一步的决策行动。

最后，在大胆假设的基础上，一定要仔细验证和考虑灰度发布是否必要，让一部分用户先试用新版本，避免出现辛普森悖论，否则可能造成不良影响。

辛普森悖论(Simpson Paradox)是由英国统计学家辛普森在1951年提出的，即在一定条件下的两组数据分开讨论时会满足一定的性质，但一旦放在一起考虑，就可能得出相反的结论。

比如A组男性1000人，女性200人，转化率分别为10%和75%。B组有200名男性和1000名女性，转化率分别为5%和50%。

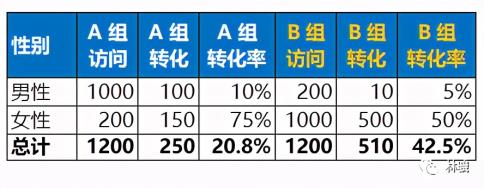
如果男女分开，A组的转化率明显高于B组，10%高于5%，75%高于50%。

但如果男女合计，A组的转化率只有20.8%，还不到B组42.5%转化率的一半。

因此，在A/B测试过程中，需要特别注意组的权重，消除组基数差异带来的影响，使测试样本真实反映总体分布。

因为数量和质量并不等价，但是，因为数量更容易衡量，人们总是习惯用数量来评价好坏，结果却可能是错过了重点。

从辛普森悖论中，我们可以得到一点启示:A做了很多不重要的小事，而B做了几件非常重要的事，最后A的成就可能远不如B。

这就是为什么我们要牢记二八法则，用20%的高效时间专注于做能产生80%效果的重要事情。临终遗言

在应用A/B测试模型时，也要遵循大事优先的原则，运用全局思维，优先考虑那些对业务影响较大的测试，而不是不分轻重缓急抓眉毛胡子一把抓。

从小到大经历过各种各样的考试，我们都有这样的经历:从0到90，从90到99，从99到100，三者花费的时间是一样的。分数越高，难度越大，效率越低。

在计算机软件开发领域，有一个“99定律”，也被称为90-90定律:

前90%的代码占用了90%的开发时间，剩下的10%的代码又占用了90%的开发时间。

在做A/B测试之前，我们可以花少量的时间快速定位正确的方向，先把细节放在一边(必要的话后期再做优化也不迟)，这样才能实现快速迭代，形成良性循环，从而获得更好的结果。